EDUBERROCAL.NET

What Is the Big Deal With GPUs?

08-November-2024

#cuda, #ai, #gpus

---

In this blog, I want to explain why GPUs are so good for Artificial Intelligence (AI), or at least for Deep Learning (DL) in general and Large Language Models (LLMs) in particular. To answer that question, let's first look at the architectural differences between CPUs and GPUs.

CPUs Versus GPUs

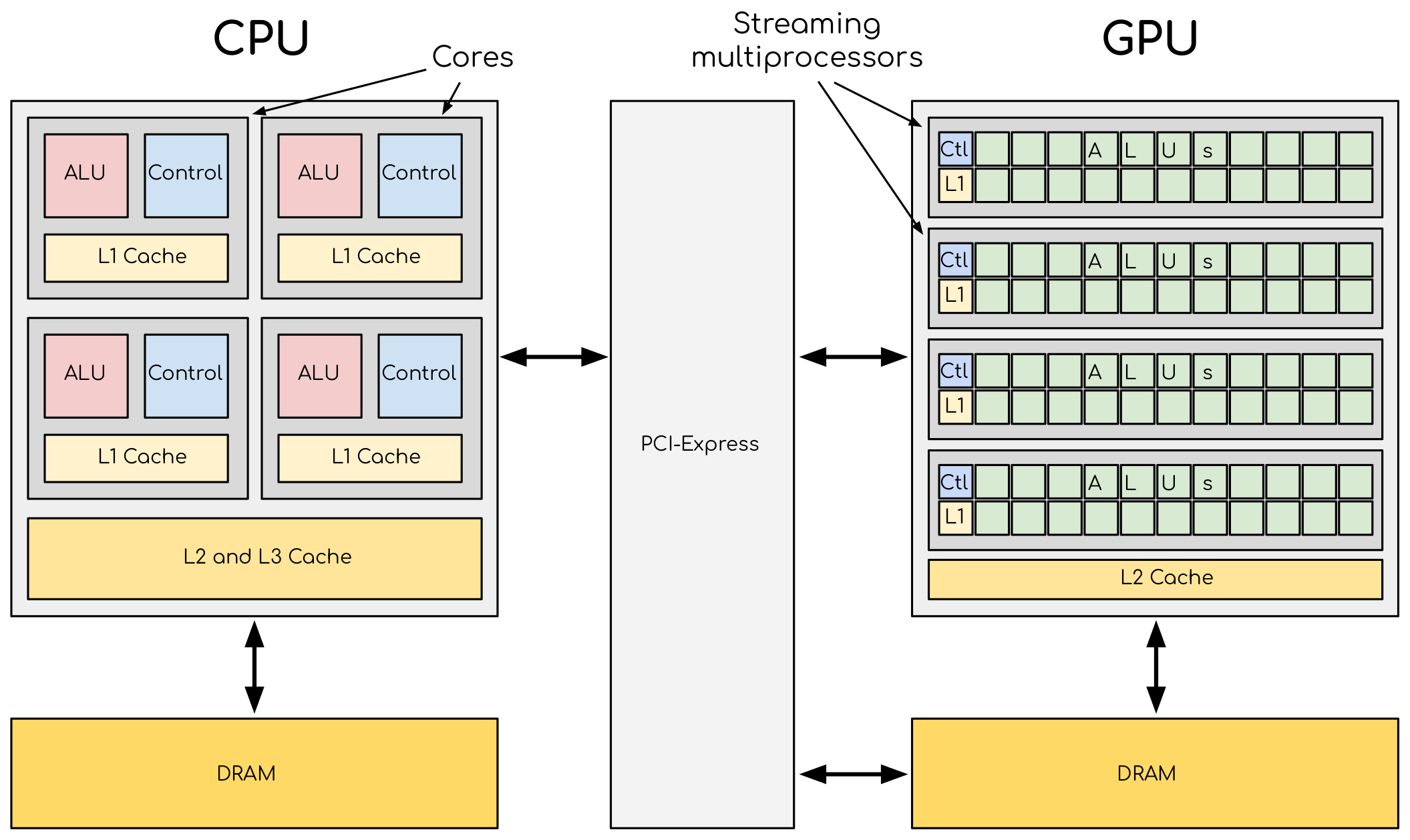
As it is possible to see, there are some significant differences. Most notably, the size and quantity of Arithmetic Logic Units (ALUs). While CPU ALUs are big and fewer, GPU ALUs are small and larger in number. Although CPU cores have supported hyper-threading (HT) for a while now (usually two virtual threads per core), we can think of an ALU in the picture as a parallel running thread. GPUs support much more parallelism than CPUs. Another difference is the size of the caches and the control logic. Again, CPUs spend more surface area on such things than GPUs.

CPU architecture has evolved to support various computing workloads, making them general-purpose computing devices. A GPU is not mandatory for a computer to work, but it certainly needs a CPU. Another key idea here is interactivity. To support interactivity, a computer should be fast and responsive. This leads us to the duality of latency vs. throughput. The first sentence from this Wikipedia article describes latency well enough: Latency, from a general point of view, is a time delay between the cause and the effect of some physical change in the system being observed. When we use our computer, for example, by moving the mouse, pressing some key in the keyboard, or executing a program, we want our actions to have low latency. If the delay between the cause and the effect is too large, user experience suffers.

CPUs have some tricks up their sleeves to support low latency. One is large caches. Caches keep recently used data--which will most likely be used again soon--in very fast memories close to the cores. Another one is pre-fetching, which brings data and instructions that will likely be used soon up the memory hierarchy. For example, if a program reads an array's contents in sequence, starting from index 0, 1, 2, and so on, it is highly likely to access elements 100, 101, 102, 103, etc. Hence, and since reading data from memory (or disk!) is so slow compared to CPU caches, it is a good strategy to cache larger chunks of data anticipating future accesses. There are more tricks, such as instruction reordering or speculative execution, but I won't go there. The point to bring home is that CPUs have very complex cores that require very complex circuits and logic. Circuits and logic that require space and power.

GPUs, on the other hand, lean more towards throughput, with more quantity of simpler cores. From here, throughput is defined as the amount of something (such as material, data, etc.) that passes through something (such as a machine or system). Throughput is more concerned about the amount of stuff passing through per unit of time than the speed a single unit of stuff needs to pass through. The way throughput beats latency is by aggregating. The best example I can think of right now is that of a car vs a bus. Cars are, in general, faster than buses. For the sake of argument, let's say that the car takes a quarter of the time to complete the same distance as the bus (15 minutes vs 1 hour). From the point of view of a single passenger, the car is better. However, the math changes considering all the passengers a bus can carry. Let's say that the bus can carry 40 people. Forty people can go from A to B in one hour. That same trajectory by car, where you can carry--let's say--four passengers each trip, would take five car hours (20 car trips x 15 mins = 5 hours. 5x slower). Consider that the car must return from B to A after each trip. We can also give passengers their own cars, but that would imply at least 10 cars (vs 1 bus), which increases cost.

Obviously, cars have other advantages. What if each passenger has a different destination? Cars are more flexible and better in that sense. In general, there isn't a silver bullet. It all depends on what you want to accomplish and the constraints. Another extreme example is that of a yacht vs a container ship.

In essence, we can say that CPUs are latency-oriented machines, while GPUs are throughput-oriented ones. For example, while CPU threads can execute different programs in parallel, GPU streaming multiprocessors (SMs) are what are called Single Instruction Multiple Threads (SIMT) processors. In SIMT, a group of threads execute the same instruction over different parts of the same (very large) dataset. It does not matter if executing a single instruction takes longer in the GPU since its power relies on numbers. A larger chunk of data can be processed per unit of time in the GPU vs the CPU. You may think that quality trumps quantity, but sometimes quantity has a quality all its own.

It Is All About Matrices (And Vectors)

It is not a mystery to anyone who hasn't been living under a rock during the last couple of years (since the launch of chatGPT) how important high-end GPUs have become, to the point where Nvidia capitalization has increased almost 9x in two years (from November/2022 to November/2024). This AI boom has been driven mostly by the power of LLMs, which require machines that can perform matrix and vector multiplications, among other operations, over massive amounts of data. The interesting part here is that these operations have little dependencies among themselves. In computing this is called an embarrassingly parallel workload, where operations can be done in parallel with little synchronization. This is exactly the type of workload that GPUs--with their SMs--excel at.

Let's look at the basic software parts required for LLM computation at a high level. I will not go into training vs. inference here, although the software pieces are the same. The difference lies mainly in the amount of computation needed, which is larger in training given that more data is used and model parameters must be updated (i.e., "learned").

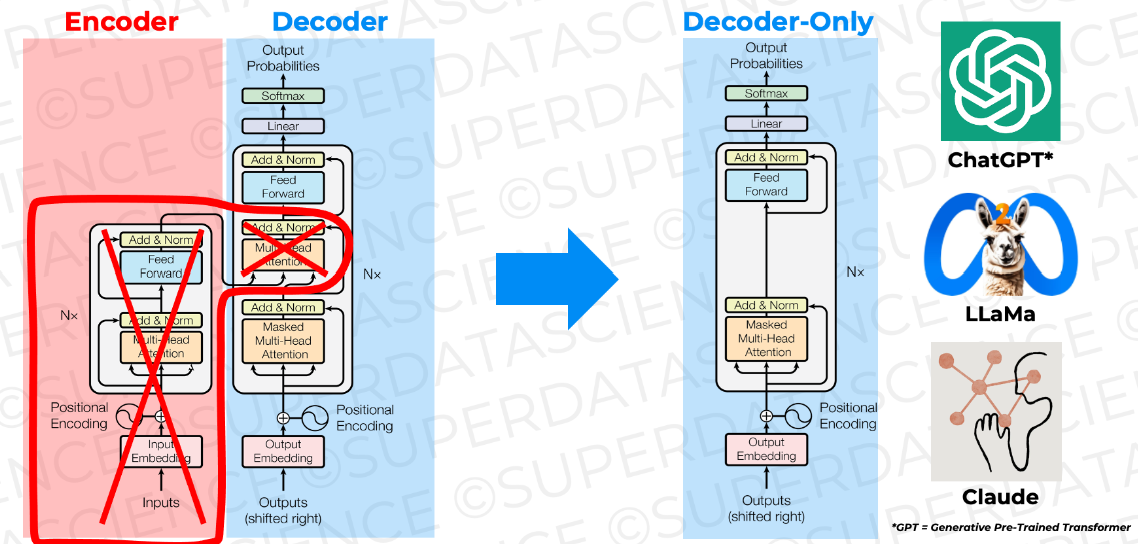
The left part of the image represents the architecture from the original Google paper where the revolutionary concept of transformers was introduced. Although that architecture was designed for applications doing language translation, one can see on the right side of the image that the generative part is already there as part of the decoder piece. If you think about it, AI-aided translation, which requires understanding the grammar, semantics, and context of words within a text, is already doing generative AI: it has to "generate" the right word for a particular context in the language of choice. For that, it uses both the input text in the original language and the already partially translated text. All that is needed for the models to be pure generative is to remove the encoder part and improve/expand the decoder to do just word generation.

Looking closely at the image, you will see some components embedded inside a white box with the label Nx. Thanks to Positional Enconding, the operations inside are performed per every word in the input (which includes the original input plus the already generated output text) in parallel. Positional encoding is one of the most powerful features of transformers, freeing up scalability by removing the need to process words sequentially (one after the other). Nx grows until some pre-defined maximum window, where the text is simply "shifted right," i.e., the oldest word is discarded at the beginning, and the newly generated word is added at the end.

Looking at the image again, we can see the different boxes with names such as Masked Multi-Head Attention or Feed Forward. I will not explain those here, although some names are self-explanatory. For more info, refer to the Google paper linked above--or ask ChatGPT :-). The idea to take home is that the whole thing is full of vector and matrix operations (input words are transformed into vectors during Embedding). Positional Encoding does vector additions, Masked Multi-Head Attention does matrix multiplication, dot-products over vectors, and vector additions, and Feed Forward Neural Networks are all about matrix multiplications.

What About Some Numbers?

To understand why, with numbers, GPUs are so much better at matrix operations--and, by extension, at generative AI--than CPUs, I ran some simple matrix multiplication experiments. Now, consider that these results are not to be generalized and used as a guide for how much better a GPU is compared to a CPU. Firstly, because the CPU used--an Intel Core i3-2120 (Sandy Bridge)--was released in 2011 while the GPU--an Nvidia GeForce GT 710--was released in 2014. I am sure that a 2014 CPU would have performed somewhat better. Also, the CPU model is a low-end/low-power SKU designed for desktops and tablets (not for servers or workstations). However, I must admit that the GPU is also low-end and low-power.

The following C snippet shows how matrix multiplications are computed sequentially using the CPU with the typical naive algorithm. The algorithm only computes the multiplication of square matrices (NxN) and has a complexity of O(N^3). For the complete code, go here:

The following are the runtimes for two matrix sizes (N=1000 and N=4000) running with a single thread versus running with four threads. The CPU used has two HT cores, totaling four threads.

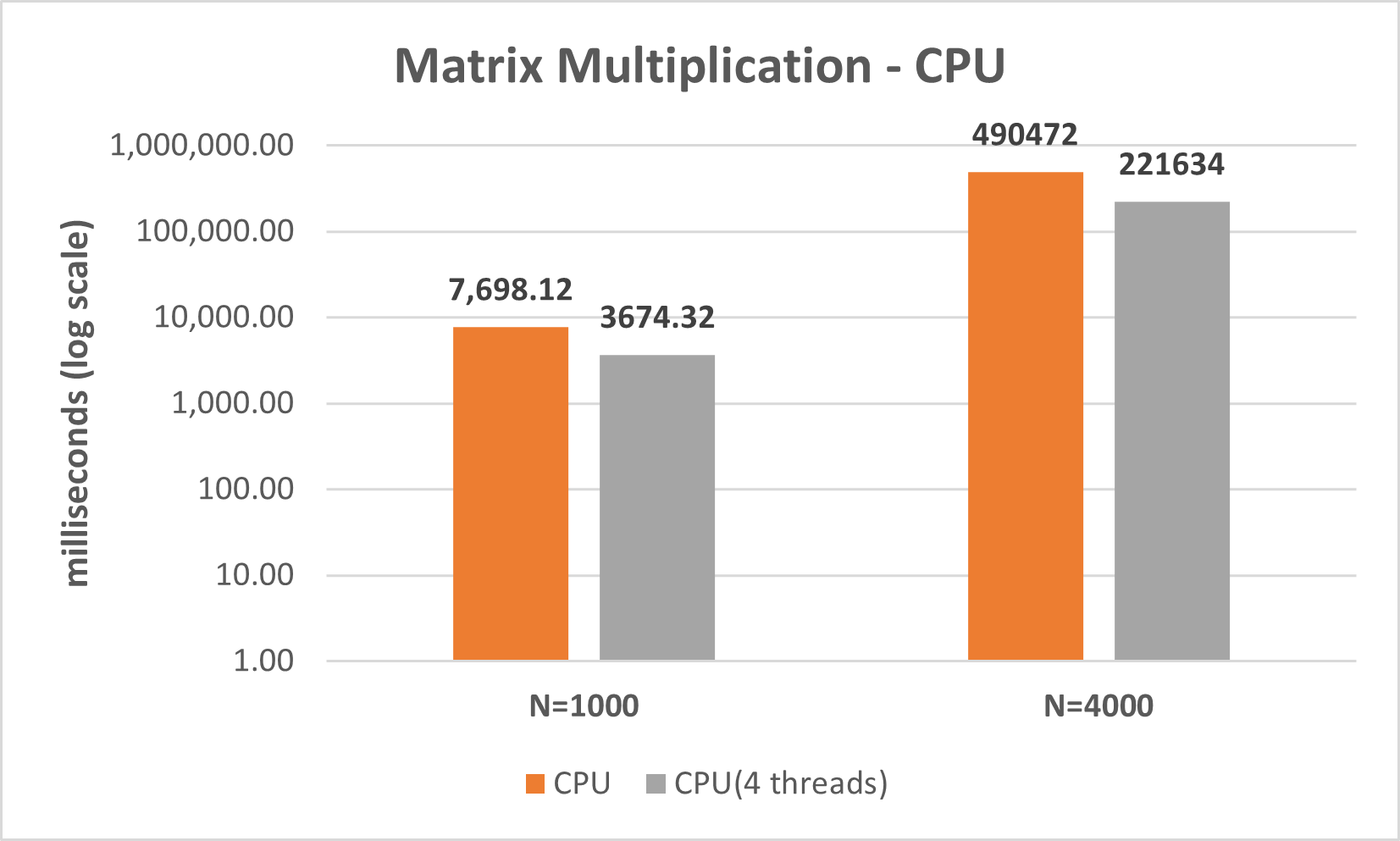
Realize that the plot is in log scale. Going from N=1000 to N=4000 using a single thread increases the time from ~7.6k milliseconds (~7.6 seconds) up to ~490k milliseconds (~1 hour and 35 minutes). We can also see that using 4 threads cuts the runtime by a little over 50% in both cases (not 75%), which makes sense if we think that matrix multiplication is CPU-intensive.

I didn't try doing N=8000 or beyond because execution time was getting out of control, and I didn't want to wait that long :-).

The following C snipped shows the CUDA kernel (a special function that runs on a GPU) doing the matrix multiplications:

I will not go into the details of CUDA programming here, but one thing to notice about this code, as compared to the sequential one, is that it has one loop as opposed to three nested ones, which gives a complexity of O(N) instead of O(N^3).

Matrix multiplication is done by multiple instances of the same kernel running on different SMs inside the GPU, performing the same instructions on different parts of the data. The part of the data that every kernel must work on is determined by the special variables blockDim and blockIdx. These variables can divide the threats in three dimensional blocks and are calculated at invocation time and passed by the CPU code:

In my case, dimBlock is set to (32, 32, 1), which gives me 32x32=1024 threads per block (I use two dimensions because my data is two-dimensional). The parameter dimGrid is set to the number of blocks, which is (ceil(N/32), ceil(N/32), 1). The ceil() function is needed because N may not be divisible by 32. If N is not divisible by 32, there will be some blocks with less data to work on than threads doing the work. In our case, for example, for N=1000 we have 1000/32=31.25 and ceil(31.25)=32, and for N=4000 we have 4000/32=125 and ceil(125)=125. So, when working with N=1000, out of the 1024 blocks, we have 63 problematic blocks: 62 blocks with 25% of valid data and one block with only 6.25%.

That is why we have to check if the positions calculated for the running thread--posx and poxy--are within the boundaries of the inputted data with the condition posx < n && posy < n. GPUs are SIMT processors, so when a thread is not within the boundaries, it will execute NOPs (i.e., blank instructions) while the other threads will execute real instructions on real data.

Here are the GPU numbers comparing them with the CPU ones (4 threads):

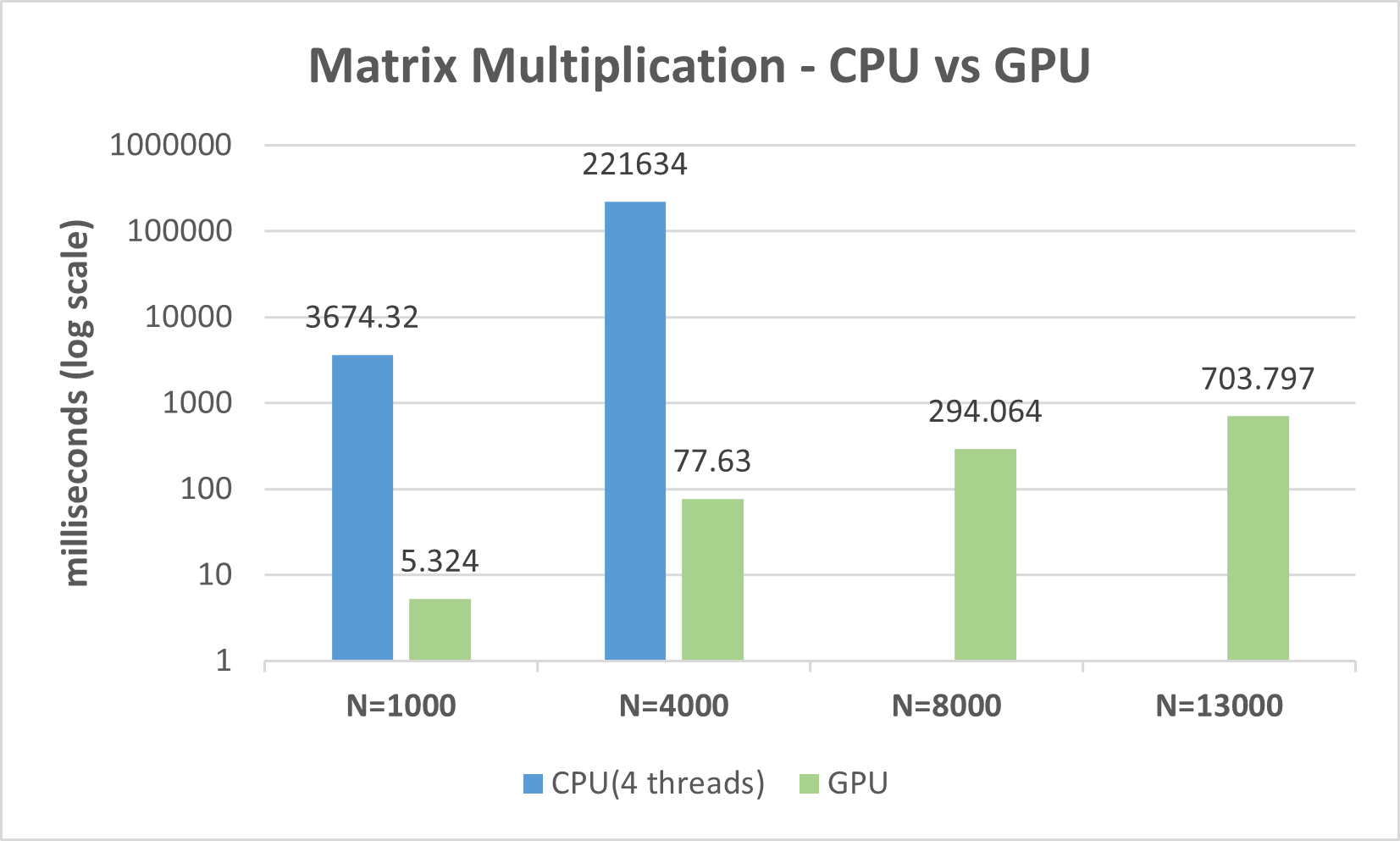
Again, the plot is in log scale. The last data point is N=13000 because N=16000 gave me out-of-memory errors in my GPU. Theoretically, we can run larger problems by dividing the input data and running the GPU multiple times. However, for the sake of time and size of this blog, I will leave that for the future.

The GPU's advantage is crystal clear. All runs finish within a second! The speedup is 690X for N=1000 and 2,855X (!!) for N=4000.

Conclusions

As I pointed out earlier, the quantity of the numbers is not important here. For example, x86 CPUs have instruction set extensions adding vector instructions that can execute the same operation over multiple registers at once that can be used to increase the speed of matrix multiplications as well, and they weren't used here (at least not explicitly; I didn't check if my compiler added them by default). The CPU used here has SSE and AVX.

CPUs have improved significantly in recent years, enlarging the size of vector instructions (AVX512), adding special instructions for DL (VNNI), and adding matrix instructions (AMX), which perform operations over chunks of matrices similar to the concept of CUDA blocks. These innovations allow CPUs to stay in the AI game for inferencing workloads or even for learning with small models.

Nevertheless, it is clear that throughput-oriented machines have the upper hand in AI overall, and they probably will in the foreseeable future.